Construction of a Symmetric Spheroform Tetrahedron

This page requires JavaScript for MathJax formatting.

Initial Definitions

Start with a positive real variable $w$ as the width (where an object's width is defined as "the distance between two parallel planes, perpendicular to the measured direction, that both touch the object's surface at at least one point without crossing its interior").

For any shape of constant width, the radius of curvature at a given point plus the radius of curvature at the opposite point always sums to $w$; let's call the maximum radius of curvature $r$ and the minimum radius of curvature $a$, where the relations $0 ≤ a ≤ r ≤ w$ and $r + a = w$ are always true.

We can define a shape-factor $0 ≤ c ≤ 1$ that controls how far the object is from a sphere, a.k.a. how different the minimum and maximum radii of curvature are from each other (at $c = 0$ we have $r = a$, so the curvature is constant, so the object is a sphere; at $c = 1$ we have $a = 0$ and $r = w$, the maximum difference possible between $r$ and $a$). The curvature variables are thus defined in terms of $w$ and $c$ as $r := \frac{w}{2} × (1 + c)$ and $a := \frac{w}{2} × (1 − c)$.

Base Tetrahedron

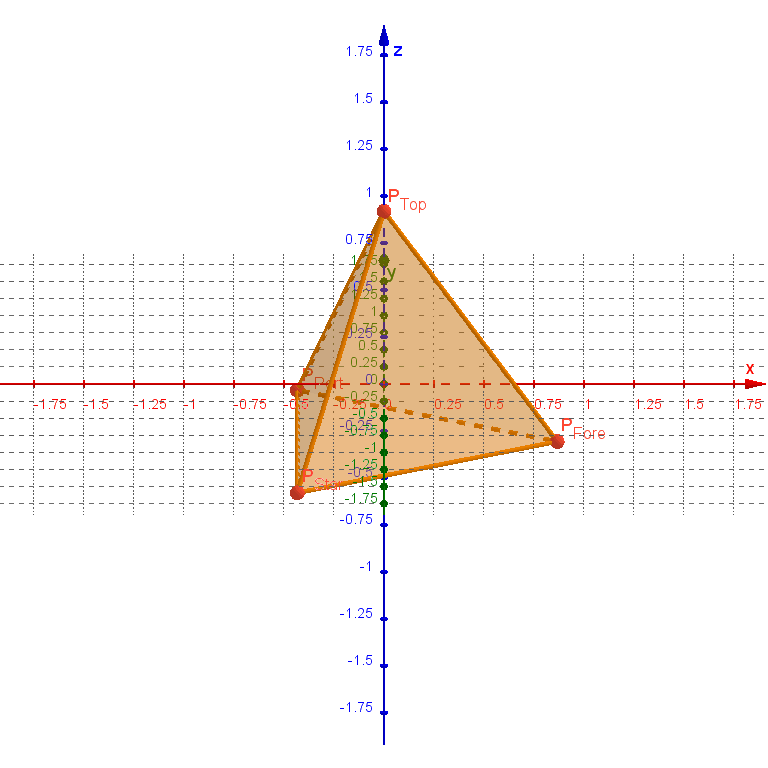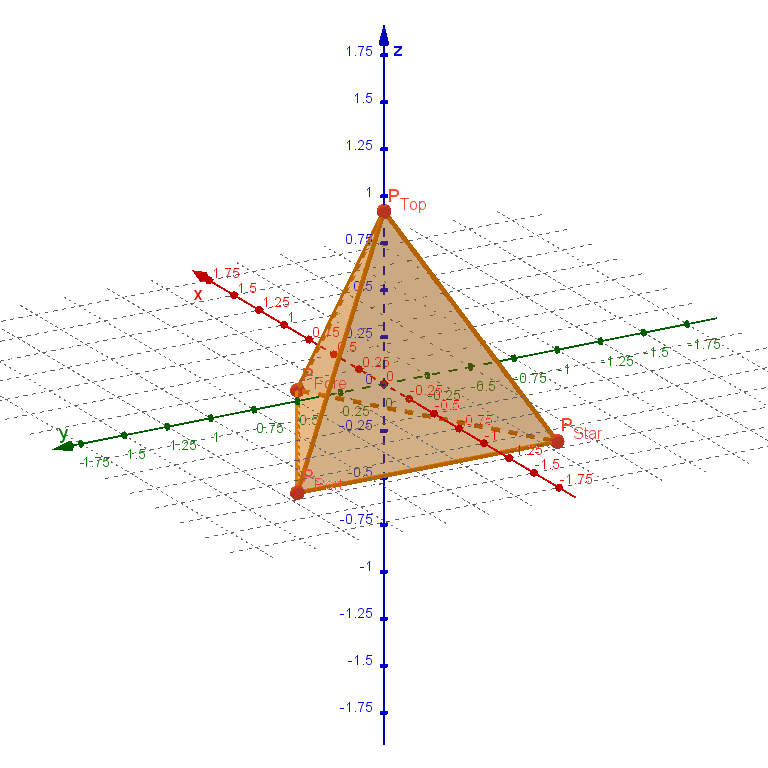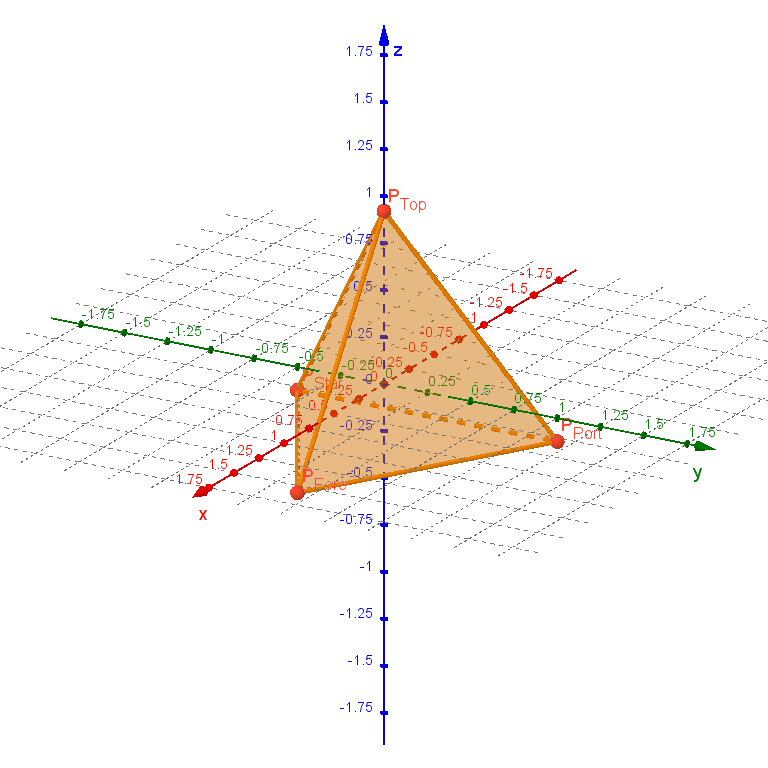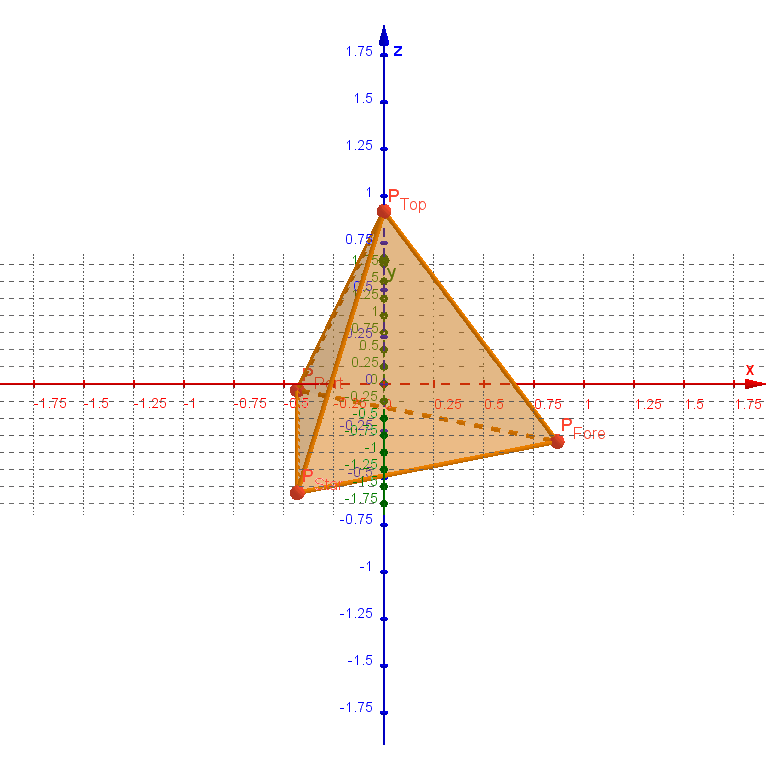
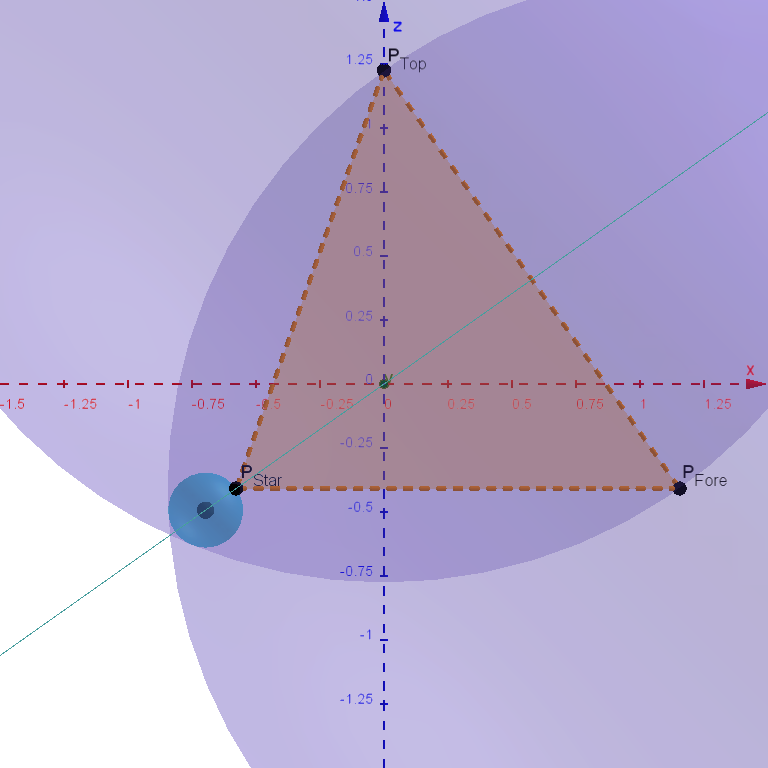
The base tetrahedron is placed with its centroid at the origin, its top vertex on the positive $z$-axis, and its front vertex in the $xz$-plane. The side length $s$ of the tetrahedron is related to the above variables by the equation $s = r − a = w × c$. Its vertices have the following positions:

$$ \begin{alignat*}{1} P_{Top} &:= s × \left(\mspace{44mu} 0, \mspace{21mu} 0, \mspace{14mu} \frac{3}{2 \sqrt{6}}\right) \\ P_{Fore} &:= s × \left(\mspace{23mu}\frac{1}{\sqrt{3}}, \mspace{21mu} 0, −\frac{1}{2 \sqrt{6}}\right) \\ P_{Port} &:= s × \left( −\frac{1}{2 \sqrt{3}}, \mspace{14mu} \frac{1}{2}, −\frac{1}{2 \sqrt{6}}\right) \\ P_{Star} &:= s × \left( −\frac{1}{2 \sqrt{3}}, −\frac{1}{2}, −\frac{1}{2 \sqrt{6}}\right) \end{alignat*} $$

The following graphic uses the parameter values $w = 2$ and $c = 0.75$:

Constructing the Edges Geometrically

A sphere with radius $s$ centered at one vertex of the tetrahedron will have the remaining three vertices lie exactly on its surface. To construct the base-aft edge-surface, start by placing one such sphere $S_{Top}$ centered on $P_{Top}$ and another such sphere $S_{Fore}$ centered on $P_{Fore}$. For any point along the tetrahedron's base-aft side (between $P_{Port}$ and $P_{Star}$), there exists a small sphere $S_{u}$ that is simultaneously tangent to the base-aft side, to $S_{Top}$, and to $S_{Fore}$; the centerpoint of $S_{u}$ always lies on the plane $z = \frac{x}{\sqrt{2}}$, which contains the base-aft side and perfectly bisects the tetrahedron.

In the following graphic, $S_{u}$ is positioned with its center on the $xz$-plane, and the orthographic camera is looking straight down the $y$-axis:

The envelope of all possible $S_{u}$ positions (a canal surface) forms the edge-surface of a tetrahedrally-symmetrical surface of constant width. Uniformly expanding the edge-canal-surface and face-spheres by a distance $a$ in the surface normal direction, and placing additional vertex-spheres of radius $a$ at each vertex of the tetrahedron, produces the final surface with width $w$.

Constructing the Edges Algebraically

To algebraically represent the sphere $S_{u}$, start with a parameter $−1 ≤ u ≤ 1$ that will control the position of $S_{u}$ between the two extremes of its travel. Let us say that $u = −1$ corresponds to $S_{u}$ being located at $P_{Star}$, $u = 0$ corresponds to $S_{u}$ being exactly centered, and $u = 1$ corresponds to $S_{u}$ being located at $P_{Port}$. The radius $ρ$ of $S_{u}$, and thus its distance from both the face-spheres and from the tetrahedron's edge, is given by the equation $ρ(u) := \sin\left(\frac{π}{8}\right)^2 × \frac{1 − u^2}{2}$. Given that radius, the two endpoints, and the fact that the centerpoint must lie on the plane $z = \frac{x}{\sqrt{2}}$, we can find that the centerpoint is located at

$$ P_{u} := s × \begin{pmatrix} −\frac{1}{2 \sqrt{3}} − \sin\left(\frac{π}{8}\right)^2 × \frac{1 − u^2}{2} × \sqrt{\frac{2}{3}}, \\ \frac{1}{2} × u, \\ −\frac{1}{2 \sqrt{6}} − \sin\left(\frac{π}{8}\right)^2 × \frac{1 − u^2}{2} × \sqrt{\frac{1}{3}} \end{pmatrix} $$

A similar process with a parameter $−1 ≤ v ≤ 1$ and the endpoints $P_{Top}$ and $P_{Fore}$ will yield the centerpoint $P_{v}$ of the opposing edge-sphere $S_{v}$ (which is always located in the $xz$-plane), though the expressions for its coordinates are longer.

Points on the base-aft canal surface can be found by starting at $P_{u}$ and moving in the direction from $P_{v}$ to $P_{u}$ by a distance of $ρ(u) + a$. Such a point has its $(x, y, z)$ coordinates defined as functions of both $u$ and $v$. Starting at $P_{v}$ and moving in the direction from $P_{u}$ to $P_{v}$ by a distance of $ρ(v) + a$ gives the points of the top-fore canal surface. The remaining four edges can be found by rotating duplicates of both canal surfaces around the $z$-axis.

To make the canal surfaces into closed shapes, instead of partial surface patches, we need to either extend the ranges of $u$ and $v$ to $±∞$, or nest the variables inside functions that turn a finite input into an infinite output. I've mostly used things like $\tan\left(\frac{π}{4} × u\right)$ over the range $−2 ≤ u ≤ 2$ in this project, as that doesn't change anything for the inputs $u = ±1$ or $u = 0$, and replacing it in turn with $\frac{\sin\left(\frac{π}{4} × u\right)}{\cos\left(\frac{π}{4} × u\right)}$ allowed opportunities to rearrange things to remove discontinuities, as seen in some of my other StackExchange questions.